Задачка для третьеклашек
Опубликовано 31 мая 2015
В репортаже ABC Eyewitness News было сказано, что эта задача разработана для восьмилетних школьников, но с ней не справляются многие взрослые. Давай посмотрим:
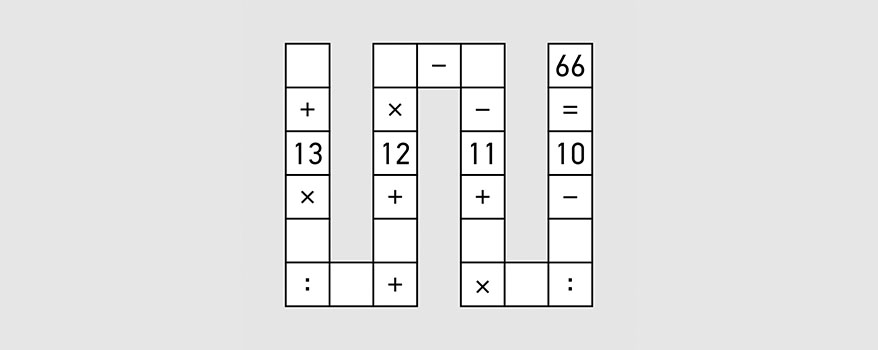
Расставь числа от 1 до 9 в пустые клетки, да так, чтобы уравнение сошлось.
Совет: сперва попробуй решить ее сам, а уже после этого смотри пост
Преимущество детей – это незнание многих правил математики. Но ты-то их знаешь. И для тебя задача становится достаточно сложной.
Первое, что может прийти в голову – это “раскручивать” задачу с конца. Напиши, если получится. Я на втором шаге сбился.
Второе – искать решения подбором. Но это неинтересно и не даст понимания происходящего.
Попробуем что-нибудь еще.
Для начала давай сделаем задачу нагляднее:
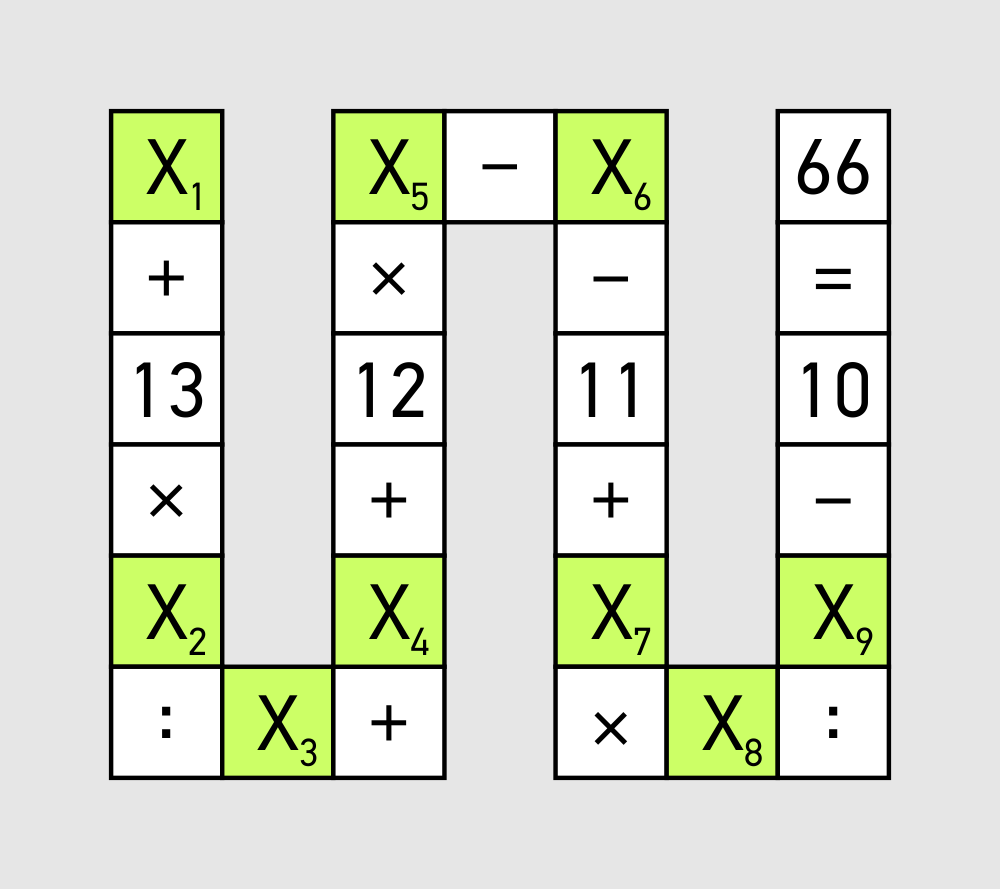
Если записать это по правилам математики, то получится уравнение с 9 переменными:
$latex \frac{\left(\left( \frac{(X_1+13 )X_2}{X_3}+X_4+12\right)X_5-X_6-11-X_7 \right)X_8}{X_9}-10=66&s=2$
Отсюда можно вывести любое неизвестное от 8 других… Вопрос: откуда брать 8 других? Все эти уравнения под спойлером. Я от этого пути отказался, но если интересно, то можешь посмотреть, вдруг тебе в голову что-то придет.
Хочу на них посмотреть
$latex X_1=-13-\frac{X_3\left(X_4-\frac{X_6-X_7+\frac{76X_9}{X_8}+11}{X_5}+12\right)}{X_2}&s=2$
$latex X_2=-\frac{X_3\left(X_4-\frac{X_6-X_7+\frac{76X_9}{X_8}+11}{X_5}+12\right)}{X_1+13}&s=2$
$latex X_3=-\frac{(X_1+13)X_2}{X_4-\frac{X_6-X_7+\frac{76X_9}{X_8}+11}{X_5}+12}&s=2$
$latex X_4=\frac{X_6-X_7+\frac{76X_9}{X_8}+11}{X5}-\frac{(X_1+13)X_2}{X_3}-12&s=2$
$latex X_5=\frac{X_6-X_7+\frac{76X_9}{X_8}+11}{\frac{(X_1+13)X_2}{X_3}+X_4+12}&s=2$
$latex X_6=X_7-\frac{76X_9}{X_8}+\left(\frac{(X_1+13)X_2}{X_3}+X_4+12\right)X_5-11&s=2$
$latex X_7=\frac{76X_9}{X_8}+\left(\frac{(X_1+13)X_2}{X_3}+X_4+12\right)X_5+X_6+11&s=2$
$latex X_8=\frac{76X_9}{\left(\frac{(X1+13)X_2}{X_3}+X_4+12\right)X_5-X_6-11+X_7}&s=2$
$latex X_9=\frac{\left(\left(\frac{(X1+13)X_2}{X_3}+X_4+12\right)X_5-X_6-11+X_7\right)X_8}{76}&s=2$
Но хочется такое решение, благодаря которому можно получить все неизвестные за раз. Немного магии, короче.
Для этого сделаем небольшую замену: $latex X_m=n_mX&s=0$. Поделим все переменные на новую переменную X. От этого все станет немного легче. Уравнение приобретет вид:
$latex \left(\left(\frac{(n_1X+13)n_2X}{n_3X}+n_4X+12\right)n_5X-n_6X-11+n_7X\right)n_8X-\\-76n_9X=0&s=2$
Раскроем скобки и наведем порядок, чтобы посмотреть, что тут вообще получилось:
$latex X(X^2(n_1n_2n_5n_8+n_3n_4n_5n_8)+\\+X(13n_2n_5n_8+12n_3n_5n_8-n_3n_6n_8+n_3n_7n_8)-\\-(11n_3n_8+76n_3n_9))=0&s=2$
Повезло – это обычное кубическое уравнение, один из коней которого равен нолю. Увы, ноль не подходит, так как в исходном уравнении появится деление на ноль. Не то, чтобы делить на ноль было нельзя. Просто сейчас это ничего не даст. Вот и обойдемся без него. И еще чуть-чуть упростим:
$latex X^2n_5n_8(n_1n_2+n_3n_4)+\\+Xn_8(n_5(13n_2+12n_3)+n_3(n_7-n_6))-\\-n3(11n_8+76n_9)=0&s=2$
И что это дало?
Корни этого уравнения, назовем их поправочными коэффициентами, помогут нам делать магию.
Как?
Шаг 1. Берем 9 случайных чисел. Это будут коэффициенты от $latex n_1&s=0$ до $latex n_9&s=0$, соответственно.
Шаг 2. На основе этих коэффициентов пытаемся найти корни уравнения, если действительных корней не нашлось (дискриминант отрицательный), то повторяем шаг 1.
Шаг 3. Умножаем коэффициенты от $latex n_1&s=0$ до $latex n_9&s=0$ на один из корней и получаем одно из возможных решений.
$latex X_m=n_mX&s=0$
Есть тут одна загвоздочка… Решения не всегда получаются целыми числами от 1 до 9. Один из лучших вариантов, когда один из корней $latex X=1&s=0$, тогда, если коэффициенты $latex n_1&s=0$ до $latex n_9&s=0$ были целыми, то и корни будут целым. Вот пример таких коэффициентов:
(3, 1, 1, 1, 3, 1, 1, 1, 1)
P.S. Формулы никак не хотели становится в одну строку, поэтому имеют многоэтажный вид.